Breadth First Search (BFS) and Depth First Search (DFS)

Graph Data Structure can be used to represent networks (like social network) or relationships between one element to another. So for example if the Graph below was representing a social networking site then you can say a Person 0 has Person 1 and Person 4 as connections. Person 1 in turn has Person 0,2,3 and 4 as its connections and so forth.

Breadth First Search(BFS) and Depth First Search(DFS) are two graph traversing algorithms. When traversing a graph there are two terminologies that are used, visit a vertex and explore a vertex.  To visit a vertex simply means to go to that vertex. To explore a vertex means to find out what are the other vertices to which the current vertex is connected to.

Breadth First Search(BFS)

In Breadth First Search (BFS) we visit and explore each vertex as we go along. Lets do a BFS of the graph shown in the picture below.
 
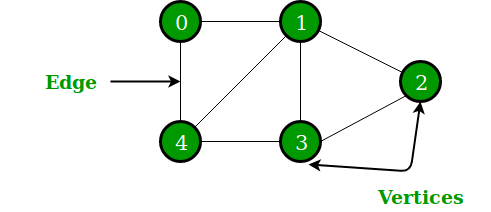
  1.  If 0 is our starting vertex then in BFS we visit 0 and then explore the neighbors of 0 which are 1 and 4. So our set of vertices are {0, 1, 4}.
  2. Next we are visiting 1 (or 4) and explore neighbors of 1 which are 0,2,3,4. Now that 0 and 4 are already part of the set of vertices we will not include them ,so our set looks like this {0,1,4,2,3}
  3. Visit 2 and explore its neighbors. Its neighbors are 1 and 3. since we already explored 1 and 3 we skip these vertices {0,1,4,2,3}.
  4. Visit 3, neighbors are 1,2 and 4 - all of them are already visited so skip them. Our set still remains{0,1,4,2,3}.
  5. Visit 4, neighbors are 0,1 and 3 -  all of them are already visited so skip them. Our set still remains {0,1,4,2,3}.

Implementation of BFS JavaScript:

// JavaScript program to print BFS nodes from a given starting vertex. 
// Adjacency List representation of the above Graph 
const adjacencyList = new Map();
adjacencyList.set(0, new Set([1,4]));
adjacencyList.set(1, new Set([0,4,2,3]));
adjacencyList.set(2, new Set([1,3]));
adjacencyList.set(3, new Set([1,4,2]));
adjacencyList.set(4, new Set([3,0,1]));


const visit = console.log;

const bfs     = (startNode) => {
const visited = new Set();
const queue   = [];
queue.push(startNode);
visited.add(startNode);

while (queue.length > 0) {
   const currentNode = queue.shift();
   visit(currentNode);
   for (let neighbor of adjacencyList.get(currentNode)) {
       if (!visited.has(neighbor)) {
            queue.push(neighbor);
            visited.add(neighbor);
      	}
    }
 }
 };

Practical Application of BFS

BFS can be used in scenarios where we have to explore closer to starting point before we go further. A good example is a GPS system where you need to find the fastest route to your destination based on the starting point. Your starting point can be the starting vertex and destination the last vertex. The different routes to the destination can be represented as edges with weights assigned based on traffic, speed limit, road work etc. Now to find the fastest route we will traverse the edges which has least amount of weights assigned to it.

Depth First Search (DFS)

In Depth First Search (DFS) we visit the nodes traversing one path on a graph until there is no more vertex to visit and then we start exploring the neighbors. Lets do a DFS of the graph shown in the picture below.
 
  1. If 0 is the starting vertex and we if we are traversing the top edges then we will visit {0,1,2}.
  2. Next we explore 2, whose neighbors are 1 and 3. So our set becomes {0,1,2,3}. Note that we skipped 1 since it is already in the set of vertices so we need not repeat it.
  3. Then we explore 1, whose neighbors 2,3 and 4. So our set becomes {0,1,2,3,4}.
  4. Then we explore 0, whose neighbors 1 and 4. Since we already have 1 and 4 in our set of vertices the final result looks like this {0,1,2,3,4}.
// JavaScript program to print DFS nodes from a given starting vertex. 
// Adjacency List representation of the above Graph 
const adjacencyList = new Map();
adjacencyList.set(0, new Set([1,4]));
adjacencyList.set(1, new Set([0,2,3,4]));
adjacencyList.set(2, new Set([1,3]));
adjacencyList.set(3, new Set([1,2,4]));
adjacencyList.set(4, new Set([0,1,3]));
const visit = console.log;
const visited = new Set();
const dfs = (node) => {
  visit(node);
  visited.add(node);
  for (let neighbour of adjacencyList.get(node)) {
    if (!visited.has(neighbour)) {
     dfs(neighbour);
    }
  }
};

Practical Application of DFS

DFS can be used in games like solving a maze, artificial intelligence or web crawlers where we need to exhaust all possible combinations before making the next move.

Time complexity of BFS and DFS

The Time complexity of both BFS and DFS are the same. If Adjacency List is used then it is O(V+E). If Adjacency Matrix is used then it is O(V2).  'V' is the number of vertices and E is the number of Edges.
Useful Link: